Debye decomposition resistivities

complex

\hat{\rho}(\omega) &= \rho_0 \left(1 - \sum_{i=1}^{N} m_k \left[1 - \frac{1}{1 + i \omega \tau_i}\right] \right)\\

real and imaginary parts

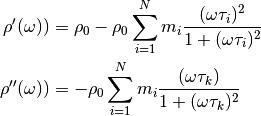
\rho'(\omega)) &= \rho_0 - \rho_0 \sum_{i=1}^N m_i \frac{(\omega \tau_i)^2}{1 + (\omega \tau_i)^2}\\ \rho''(\omega)) &= - \rho_0 \sum_{i=1}^N m_i \frac{(\omega \tau_k)}{1 + (\omega \tau_k)^2}

Derivatives

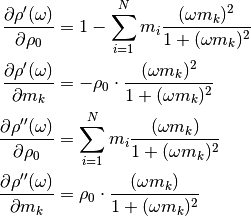
\frac{\partial \rho'(\omega)}{\partial \rho_0} &= 1 - \sum_{i=1}^N m_i \frac{(\omega m_k)^2}{1 + (\omega m_k)^2}\\ \frac{\partial \rho'(\omega)}{\partial m_k} &= -\rho_0 \cdot \frac{(\omega m_k)^2}{1 + (\omega m_k)^2}\\ \frac{\partial \rho''(\omega)}{\partial \rho_0} &= \sum_{i=1}^N m_i \frac{(\omega m_k)}{1 + (\omega m_k)^2}\\ \frac{\partial \rho''(\omega)}{\partial m_k} &= \rho_0 \cdot \frac{(\omega m_k)}{1 + (\omega m_k)^2}\\

Relating peak frequency of imaginary part to relaxation time

Notes:

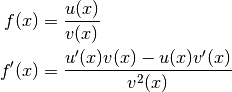
f(x) &= \frac{u(x)}{v(x)}\\ f'(x) &= \frac{u'(x) v(x) - u(x) v'(x)}{v^2(x)}

Determine the frequency maximum of the negative of the imaginary part using the first derivation:

Im(\hat{\rho}(\omega)) &= - \rho_0 \sum_{i=1}^N m_i \frac{(\omega \tau_k)}{1 + (\omega \tau_k)^2}\\ \frac{\partial Im}{\partial \omega} &= \frac{\partial \omega (-\rho_0 m \omega \tau) [1 + (\omega \tau)^2] - (-\rho_0 m \omega \tau) \partial \omega (1 + (\omega \tau)^2)}{[1 + (\omega \tau)^2]^2}\\

&= \frac{(-\rho_0 m \tau) [1 + (\omega \tau)^2] + \rho_0 m \omega \tau \cdot 2 \omega \tau \tau}{[1 + (\omega \tau)^2]^2}\\ \Rightarrow \frac{\partial -Im}{\partial \omega} &= 0\\ &\Leftrightarrow - \rho_0 m \tau - \rho_0 m \tau (\omega \tau)^2 + 2 \omega^2 \tau^3 m \rho_0 = 0\\ & / \tau / \rho_0 / m\\

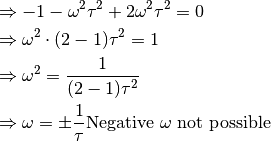
&\Rightarrow -1 - \omega^2 \tau^2 + 2 \omega^2 \tau^2 = 0\\ &\Rightarrow \omega^2 \cdot (2 - 1) \tau^2 = 1\\ &\Rightarrow \omega^2 = \frac{1}{(2-1) \tau^2}\\ &\Rightarrow \omega = \pm \frac{1}{\tau} \text{Negative } \omega \text{ not possible}\\

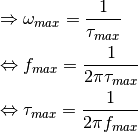
&\Rightarrow \omega_{max} = \frac{1}{\tau_{max}}\\ &\Leftrightarrow f_{max} = \frac{1}{2 \pi \tau_{max}}\\ &\Leftrightarrow \tau_{max} = \frac{1}{2 \pi f_{max}}\\

Peak relaxation times

Peak relaxation times for the conductivity (a.k.a. Cole-Cole, CC) and the resistivity (a.k.a. Pelton, P) formulation are related by:

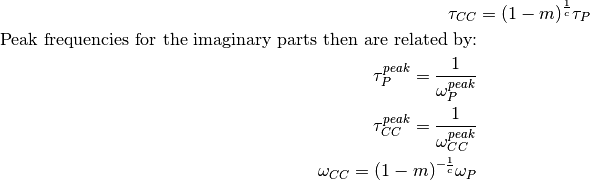
\tau_{CC} &= (1 - m)^{\frac{1}{c}} \tau_P\\ \text{Peak frequencies for the imaginary parts then are related by:}\\ \tau_{P}^{peak} = \frac{1}{\omega_{P}^{peak}}\\ \tau_{CC}^{peak} = \frac{1}{\omega_{CC}^{peak}}\\ \omega_{CC} = (1 - m)^{-\frac{1}{c}} \omega_{P}

The relation hold for both the Cole-Cole model and the Debye model (c=1). Additionally, they also hold for the decomposition approach, here the chargeability has to be replaced by the total chargeability: 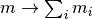m \rightarrow \sum_i m_i.