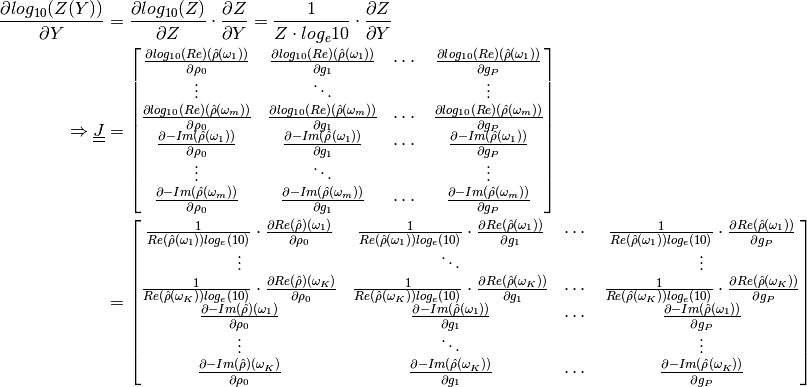Inversion and implementation details

Inversion

The forward model is formulated using the real and imaginary parts, and is a real valued function by stacking real and imaginary part on top of each other, i.e. by doubling the data space.

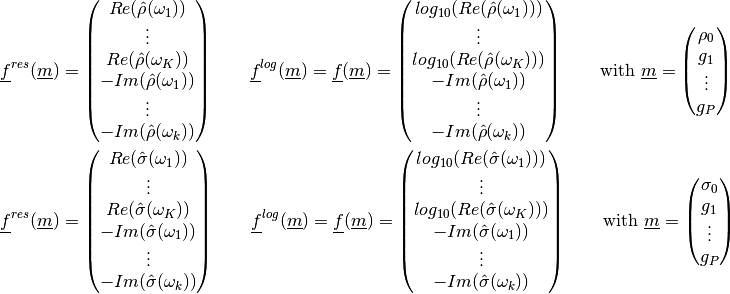
\underline{f}^{res}(\underline{m}) &= \begin{pmatrix}Re(\hat{\rho}(\omega_1))\\ \vdots \\ Re(\hat{\rho}(\omega_K))\\ -Im(\hat{\rho}(\omega_1))\\ \vdots \\ -Im(\hat{\rho}(\omega_k))\end{pmatrix} \quad \quad \underline{f}^{log}(\underline{m}) = \underline{f}(\underline{m}) = \begin{pmatrix}log_{10}(Re(\hat{\rho}(\omega_1)))\\ \vdots \\ log_{10}(Re(\hat{\rho}(\omega_K)))\\ -Im(\hat{\rho}(\omega_1))\\ \vdots \\ -Im(\hat{\rho}(\omega_k))\end{pmatrix} \quad \quad \text{with } \underline{m} = \begin{pmatrix} \rho_0\\ g_1\\ \vdots \\ g_P \end{pmatrix}\\ \underline{f}^{res}(\underline{m}) &= \begin{pmatrix}Re(\hat{\sigma}(\omega_1))\\ \vdots \\ Re(\hat{\sigma}(\omega_K))\\ -Im(\hat{\sigma}(\omega_1))\\ \vdots \\ -Im(\hat{\sigma}(\omega_k))\end{pmatrix} \quad \quad \underline{f}^{log}(\underline{m}) = \underline{f}(\underline{m}) = \begin{pmatrix}log_{10}(Re(\hat{\sigma}(\omega_1)))\\ \vdots \\ log_{10}(Re(\hat{\sigma}(\omega_K)))\\ -Im(\hat{\sigma}(\omega_1))\\ \vdots \\ -Im(\hat{\sigma}(\omega_k))\end{pmatrix} \quad \quad \text{with } \underline{m} = \begin{pmatrix} \sigma_0\\ g_1\\ \vdots \\ g_P \end{pmatrix}

Jacobian

The Jacobian of \underline{f}(\underline{m}) is defined as:

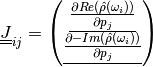
\underline{\underline{J}}_{ij} = \begin{pmatrix}\underline{\frac{\partial Re(\hat{\rho}(\omega_i))}{\partial p_j}}\\\underline{\frac{\partial -Im(\hat{\rho}(\omega_i))}{\partial p_j}}\end{pmatrix}

As such it is a (2 F x M) matrix, with F the number of frequencies and M the number of patameters.

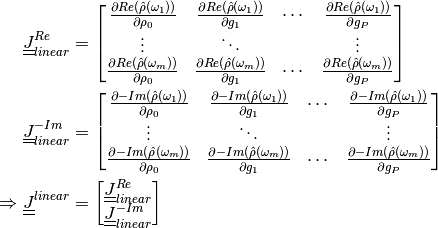
\underline{\underline{J}}^{Re}_{linear} &= \begin{bmatrix} \frac{\partial Re(\hat{\rho}(\omega_1))}{\partial \rho_0} & \frac{\partial Re(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{\partial Re(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{\partial Re(\hat{\rho}(\omega_m))}{\partial \rho_0} & \frac{\partial Re(\hat{\rho}(\omega_m))}{\partial g_1} & \cdots & \frac{\partial Re(\hat{\rho}(\omega_m))}{\partial g_P} \end{bmatrix}\\ \underline{\underline{J}}^{-Im}_{linear} &= \begin{bmatrix} \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial g_P} \end{bmatrix}\\ \Rightarrow \underline{\underline{J}}^{linear} &= \begin{bmatrix}\underline{\underline{J}}^{Re}_{linear}\\\underline{\underline{J}}^{-Im}_{linear}\end{bmatrix}

The Jacobian of 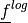\underline{f}^{log} can now be computed using the chain rule:

\frac{\partial log_{10}(Z(Y))}{\partial Y} &= \frac{\partial log_{10}(Z)}{\partial Z} \cdot \frac{\partial Z}{\partial Y} = \frac{1}{Z \cdot log_e{10}} \cdot \frac{\partial Z}{\partial Y}\\ \Rightarrow \underline{\underline{J}} &= \begin{bmatrix} \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_1))}{\partial \rho_0} & \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_m))}{\partial \rho_0} & \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_m))}{\partial g_1} & \cdots & \frac{\partial log_{10}(Re)(\hat{\rho}(\omega_m))}{\partial g_P} \\ \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_m))}{\partial g_P} \end{bmatrix}\\ &= \begin{bmatrix} \frac{1}{Re(\hat{\rho}(\omega_1)) log_e(10)} \cdot \frac{\partial Re(\hat{\rho})(\omega_1)}{\partial \rho_0} & \frac{1}{Re(\hat{\rho}(\omega_1)) log_e(10)} \cdot \frac{\partial Re(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{1}{Re(\hat{\rho}(\omega_1)) log_e(10)} \cdot\frac{\partial Re(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{1}{Re(\hat{\rho}(\omega_K)) log_e(10)} \cdot \frac{\partial Re(\hat{\rho})(\omega_K)}{\partial \rho_0} & \frac{1}{Re(\hat{\rho}(\omega_K)) log_e(10)} \cdot \frac{\partial Re(\hat{\rho}(\omega_K))}{\partial g_1} & \cdots & \frac{1}{Re(\hat{\rho}(\omega_K)) log_e(10)} \cdot\frac{\partial Re(\hat{\rho}(\omega_K))}{\partial g_P}\\ \frac{\partial -Im(\hat{\rho})(\omega_1)}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_1))}{\partial g_P}\\ \vdots & \ddots & & \vdots\\ \frac{\partial -Im(\hat{\rho})(\omega_K)}{\partial \rho_0} & \frac{\partial -Im(\hat{\rho}(\omega_K))}{\partial g_1} & \cdots & \frac{\partial -Im(\hat{\rho}(\omega_K))}{\partial g_P}\end{bmatrix}\\