Integral Parameters¶
Integral parameters extracted from the RTD fall into two categories: chargeability related values and relaxation time related values. The first category extracts information regarding the total or partial polarization strength of the system, while the second extracts information regarding relaxation times, i.e. the time scales on which the polarization processes take place:
Chargeability parameters:
The total chargeability
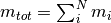 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
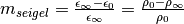 (this is also the definition used
for
(this is also the definition used
for 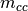 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 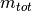 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
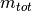 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
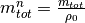 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
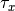 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 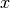 of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example,
of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example, 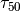 is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).
is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).Nordsiek and Weller, 2008 introduced the non-uniformity parameter
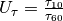 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 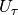 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
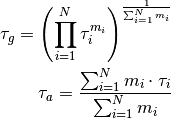
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
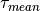
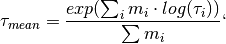
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 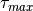 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 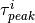 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 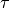 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
Chargeability parameters:
The total chargeability
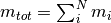 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
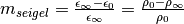 (this is also the definition used
for
(this is also the definition used
for 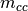 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 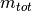 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
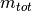 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
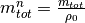 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
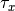 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 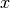 of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
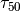 is the median relaxation time of a given RTD.
is the median relaxation time of a given RTD.Nordsiek and Weller, 2008 introduced the non-uniformity parameter
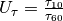 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 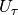 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
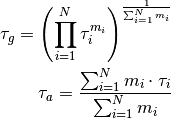
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
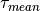
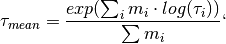
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 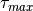 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 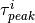 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 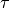 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
Integral Parameters
===================
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
Integral Parameters
===================
Integral parameters extracted from the RTD fall into two categories: chargeability related values and relaxation time related values. The first category extracts information regarding the total or partial polarization strength of the system, while the second extracts information regarding relaxation times, i.e. the time scales on which the polarization processes take place:
Chargeability parameters:
The total chargeability
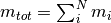 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
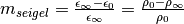 (this is also the definition used
for
(this is also the definition used
for 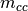 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 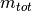 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
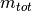 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
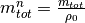 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
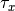 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 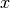 of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example,
of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example, 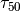 is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).
is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).Nordsiek and Weller, 2008 introduced the non-uniformity parameter
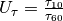 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 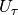 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
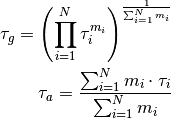
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
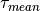
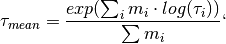
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 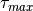 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 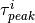 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 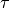 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
Chargeability parameters:
The total chargeability
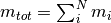 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
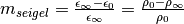 (this is also the definition used
for
(this is also the definition used
for 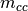 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 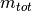 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
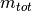 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
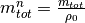 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
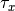 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 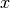 of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
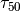 is the median relaxation time of a given RTD.
is the median relaxation time of a given RTD.Nordsiek and Weller, 2008 introduced the non-uniformity parameter
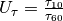 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 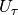 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
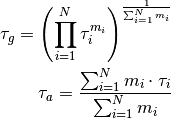
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
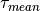
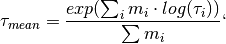
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 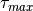 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 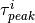 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 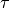 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
Integral Parameters
===================
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
Integral Parameters
===================
Integral parameters extracted from the RTD fall into two categories: chargeability related values and relaxation time related values. The first category extracts information regarding the total or partial polarization strength of the system, while the second extracts information regarding relaxation times, i.e. the time scales on which the polarization processes take place:
Chargeability parameters:
The total chargeability
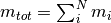 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
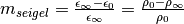 (this is also the definition used
for
(this is also the definition used
for 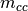 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 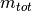 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
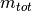 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
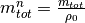 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
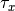 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 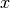 of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example,
of chargeability is reached (Norsieg and Weller,
2008; Zisser et al. 2010). For example, 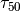 is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).
is the median
relaxation time of a given RTD. (See ref:environ_vars on how to set
individual percentages).Nordsiek and Weller, 2008 introduced the non-uniformity parameter
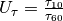 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 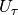 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
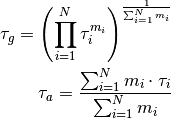
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
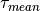
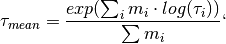
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 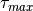 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 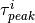 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 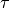 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
Integral parameters extracted from the RTD fall into two categories:
chargeability related values and relaxation time related values. The first
category extracts information regarding the total or partial polarization
strength of the system, while the second extracts information regarding
relaxation times, i.e. the time scales on which the polarization processes take
place:
Chargeability parameters:
The total chargeability
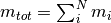 is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
is the analogon of the
DD to the chargeability as defined by Seigel, 1959:
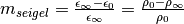 (this is also the definition used
for
(this is also the definition used
for 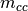 ). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by
). This is, howoever, only true insofar as the majority of
the polarisation response of the system must be located within the measured
frequency range for the DD to pick it up, while the original definition of
the chargeability extends over the whole frequency domain. Thus, not fully
resolved polarization peaks indicate an underestimation of the total
polarization of the system by 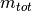 in the DD.
in the DD.Nordsiek and Weller, 2008 computed chargeability sums for each relaxation time decades, normed by
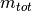 . These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.
. These so called decade
loadings provide frequency (or relaxation time) dependent chargeabilities.The total, normalized chargeability
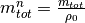 is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
is obtained by normalizing the total chargeability
with the DC resistivity (Scott2003phd, Weller2010g_a). It gives an indication
of the total polarization of the measured system without any influence of any
occuring resistivity contrasts.
Relaxation time parameters:
Various parameters to determine characteristic relaxation times from the whole RTD were proposed:
Cumulative relaxation times
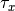 denote relaxation times at which a
certain percentage
denote relaxation times at which a
certain percentage 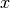 of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
of chargeability is reached
(Norsieg and Weller, 2008; Zisser et al. 2010). For example,
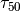 is the median relaxation time of a given RTD.
is the median relaxation time of a given RTD.Nordsiek and Weller, 2008 introduced the non-uniformity parameter
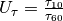 which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using
which characterizes the width of
the RTD. However, no information regarding the number of siginificant peaks
in the RTD can be derived using 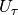 .
.Tong et al, 2004 use the arithmetic and geometric means of the relaxation times for further analysis:
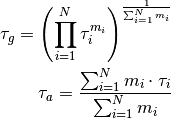
Nordsiek et al., 2008 introduced the logarithmic average relaxation time
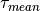
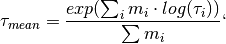
The listed relaxation time parameters do not take into account the specific
shape of the RTD, and thus it is also useful to determine local maxima of the
distribution, e.g. to extract characteristic relaxation times specific to
certain polarisation peaks. This approach has conceptual similarities to the
use of (multi-)Cole-Cole models as the produced relaxation times can be
directly related to polarization peaks. The relaxation time with the larges
corresponding chargeability is called 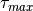 (Attwa2013hess), and the in the generalized form the
relaxation time
(Attwa2013hess), and the in the generalized form the
relaxation time 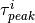 , refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high
, refers to the i-th local maximum of
the RTD, starting with the low frequencies (i.e. high 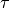 values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.
values).
This approach can recover multiple peaks without any knowlegdge of the exact
number of peaks in the data. However, this process can yield multiple small
maxima if the smoothing between adjacent chargeabilitiy values is not strong
enough. In these cases the corresponding smoothing parameters of the DD should
be increased.