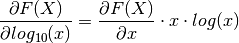Cole-Cole decomposition resistivities

complex

\hat{\rho}(\omega) &= \rho_0 \left[ 1 - \sum_k m_k \left(1 - \frac{1}{1 + (j \omega \tau_k)^c} \right) \right]

real and imaginary parts

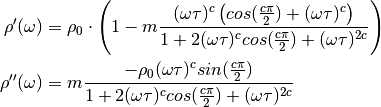
\rho'(\omega) &= \rho_0 \cdot \left(1 - m \frac{ (\omega \tau)^{c} \left(cos(\frac{c \pi}{2}) + (\omega \tau)^{c}\right)}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}\right)\\ \rho''(\omega) &= m \frac{ - \rho_0 (\omega \tau)^{c} sin(\frac{c \pi}{2})}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}

partial derivatives

There are partial derivatives of the real and the imaginary part respect to all variables.

real parts

\frac{\partial \hat{\rho'}(\omega)}{\partial \rho_0} &= 1 - \frac{m (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^c}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}\\ \frac{\partial \hat{\rho'}(\omega)}{\partial m} &= - \rho_0 m (\omega \tau)^c \frac{(cos(\frac{c \pi}{2}) + (\omega \tau)^c)}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}\\ \frac{\partial \hat{\rho'}(\omega)}{\partial \tau} &= \rho_0 \frac{-m \omega^c c \tau^{c-1} cos(\frac{c \pi}{2} - m \omega^{2 c} 2 c \tau^{2c - 1}}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}} +\\ &\rho_0 \frac{\left[m (\omega \tau)^c (cos(\frac{c \pi}{2}) + (\omega \tau)^c) \right] \cdot \left[ 2 \omega^c c \tau^{c-1} cos(\frac{c \pi}{2}) + 2 c \omega^{2 c} \tau^{2 c - 1}\right]}{\left[1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}\right]^2}\\ \frac{\partial \hat{\rho'}(\omega)}{\partial c} &= \rho_0 \frac{-m ln(\omega \tau) (\omega \tau)^c cos(\frac{c \pi}{2}) + m (\omega\tau)^c \frac{\pi}{2} sin(\frac{c \pi}{2}) + ln(\omega \tau)(\omega \tau)^c}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}} +\\ &\rho_0 \frac{\left[-m (\omega \tau)^c (cos(\frac{c \pi}{2}) + (\omega \tau)^c) \right] \cdot \left[ -2 ln(\omega \tau) (\omega \tau)^c cos(\frac{c \pi}{2}) + 2 (\omega \tau)^c \frac{\pi}{2} cos(\frac{c \pi}{2} + 2 ln(\omega \tau) (\omega \tau)^{2 c}\right]}{\left[1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}\right]^2}

imaginary parts

\frac{\partial \hat{\rho}''(\omega)}{\partial \rho_0} &= - \frac{m (\omega \tau)^c sin(\frac{c \pi}{2})}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}\\ \frac{\partial \hat{\rho''}(\omega)}{\partial m} &= - \rho_0 m (\omega \tau)^c \frac{sin(\frac{c \pi}{2})}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}}\\ \frac{\partial \hat{\rho''}(\omega)}{\partial \tau} &= \rho_0 \frac{-m \omega^c c \tau^{c-1} sin(\frac{c \pi}{2} }{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}} +\\ &\rho_0 \frac{\left[-m (\omega \tau)^c sin(\frac{c \pi}{2} \right] \cdot \left[ 2 \omega^c c \tau^{c-1} cos(\frac{c \pi}{2}) + 2 c \omega^{2 c} \tau^{2 c - 1}\right]}{\left[1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}\right]^2}\\ \frac{\partial \hat{\rho''}(\omega)}{\partial c} &= \rho_0 \frac{-m sin(\frac{c \pi}{2}) ln(\omega \tau)(\omega \tau)^c - m (\omega \tau)^c \frac{\pi}{2} cos(\frac{\pi}{2}}{1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}} +\\ &\rho_0 \frac{\left[-m (\omega \tau)^c cos(\frac{c \pi}{2}) \right] \cdot \left[ -2 ln(\omega \tau) (\omega \tau)^c cos(\frac{c \pi}{2}) + 2 (\omega \tau)^c \frac{\pi}{2} cos(\frac{c \pi}{2}) \right] + \left[2 ln(\omega \tau) (\omega \tau)^{2 c}\right]}{\left[1 + 2 (\omega \tau)^c cos(\frac{c \pi}{2}) + (\omega \tau)^{2 c}\right]^2}

Partial derivatives respect to 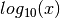log_{10}(x):

There are also partial derivatives of the real and the imaginary part respect to the common logarithm of all variables:

\frac{\partial F(X)}{\partial log_{10}(x)} &= \frac{\partial F(X)}{\partial x} \cdot x \cdot log(x)